Probability distributions

1 Binomial distribution

  • Assume \(X\) follows a binomial distribution with parameters \(n\) and \(p\), i.e., \[X\sim B(n, p)\]

  • Probability mass function \[p(x) = P(X=x) = {n \choose x}p^x (1-p)^{n-x}, x=0, 1, 2, \ldots\]

  • Cumulative distribution function \[F(x) = P(X\leq x) = \sum_{y = 0}^x P(X=y)\]

  • Consider \(B(10, 0.5)\) 
dat_binom <- tibble(
  x = 0:10,
  prob = dbinom(x = x, size = 10, prob = .5),
  cprob = cumsum(prob),
  cprob1 = pbinom(q = x, size = 10, prob = .5)
)
dat_binom
#> # A tibble: 11 × 4
#>        x     prob    cprob   cprob1
#>    <int>    <dbl>    <dbl>    <dbl>
#>  1     0 0.000977 0.000977 0.000977
#>  2     1 0.00977  0.0107   0.0107  
#>  3     2 0.0439   0.0547   0.0547  
#>  4     3 0.117    0.172    0.172   
#>  5     4 0.205    0.377    0.377   
#>  6     5 0.246    0.623    0.623   
#>  7     6 0.205    0.828    0.828   
#>  8     7 0.117    0.945    0.945   
#>  9     8 0.0439   0.989    0.989   
#> 10     9 0.00977  0.999    0.999   
#> 11    10 0.000977 1        1

Binomial distribution: PMF

ggplot(data = dat_binom) +
  geom_col(aes(x = x, y = prob))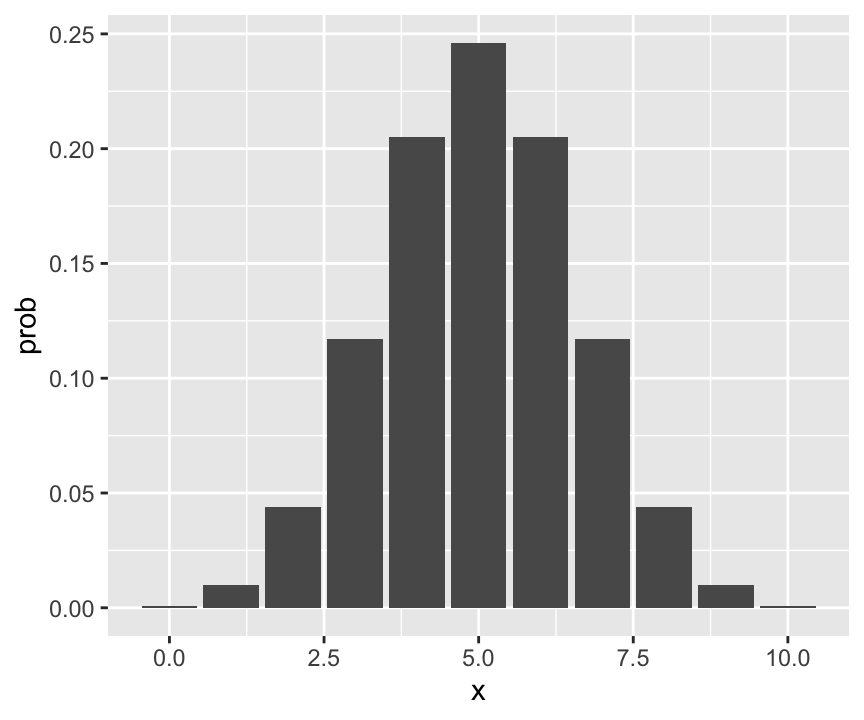

ggplot(data = dat_binom) +
  geom_col(aes(x = x, y = prob)) +
  scale_x_continuous(breaks = 0:10)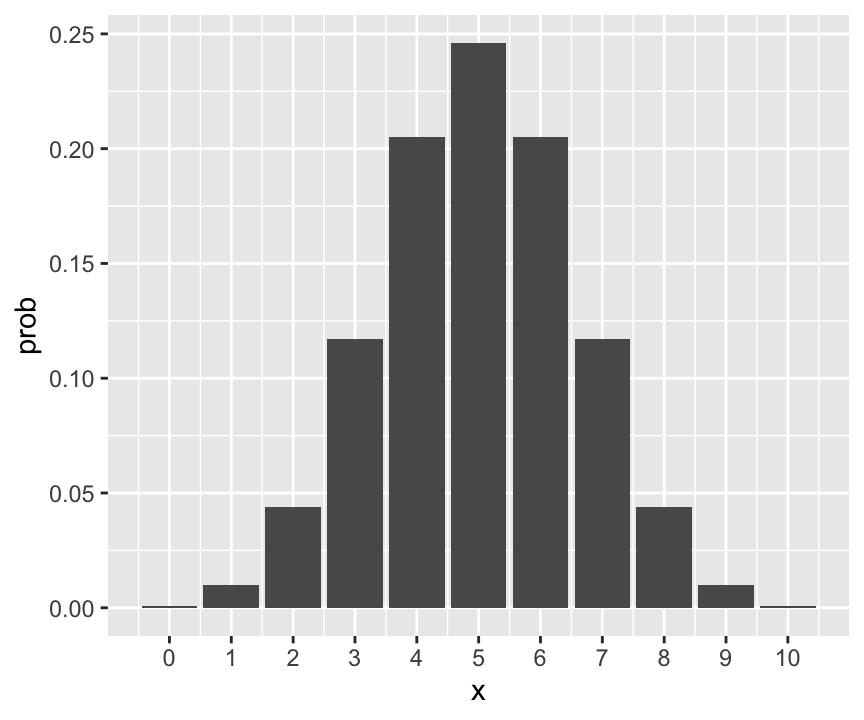 

ggplot(data = dat_binom) +
  geom_col(aes(x = x, y = prob), width = .2) + 
  scale_x_continuous(breaks = 0:10)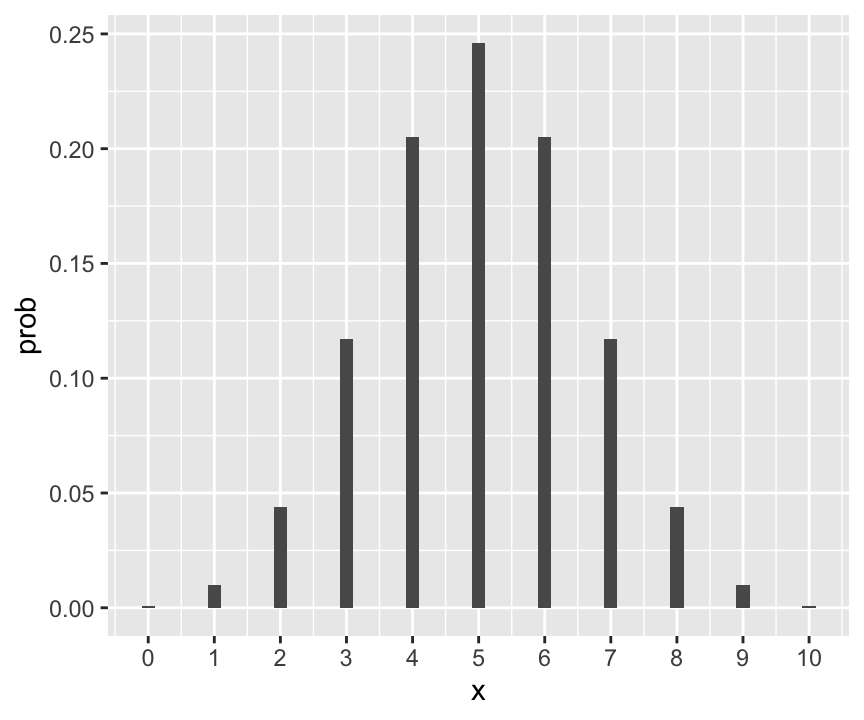

ggplot(data = dat_binom) +
  geom_col(aes(x = x, y = prob), width = .2) +
  scale_x_continuous(breaks = 0:10) +
  theme_minimal(base_size = 18)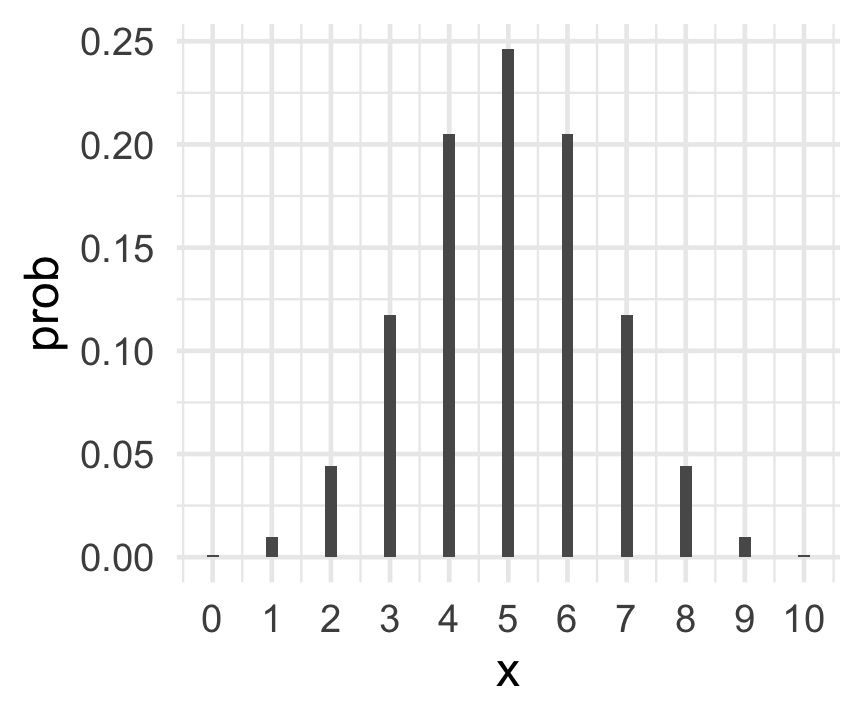

Binomial distribution: CDF

\[F(x) = P(X\leq x) = \sum_{y\leq x} P(X=y)\]

p1 <- ggplot(data = dat_binom) +
  geom_step(aes(x = x, y = cprob)) + 
  scale_x_continuous(breaks = 0:10) +
  theme_bw(base_size = 18)
p1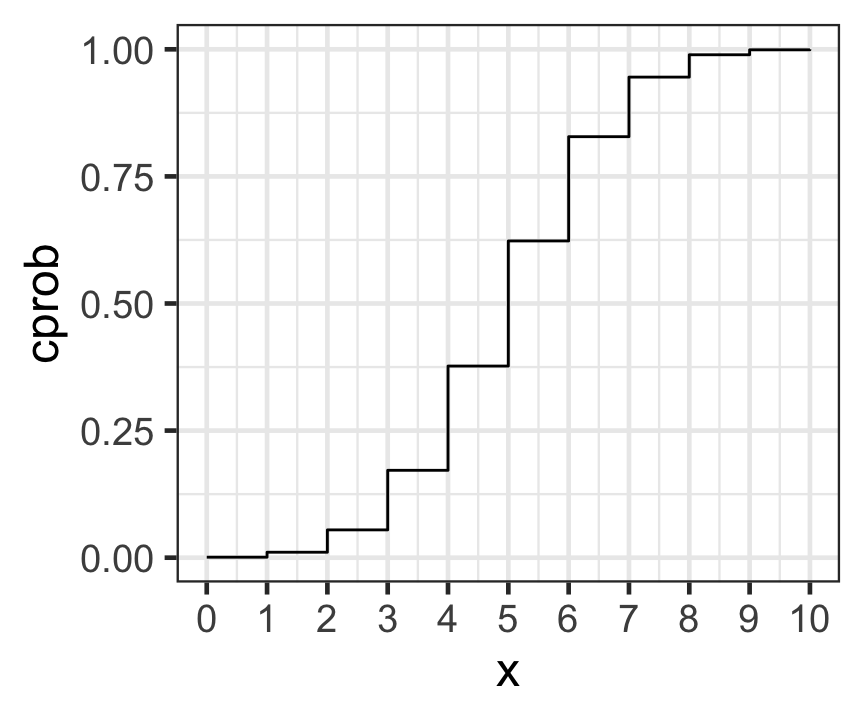

dat1 = tibble(x = dat_binom$x[-1], 
              y = dat_binom$cprob[-11])
#
p1 + 
  geom_point(aes(x = x, y = cprob), size = 4) + 
  geom_point(data = dat1, aes(x = x, y = y), 
             shape=1, size = 3)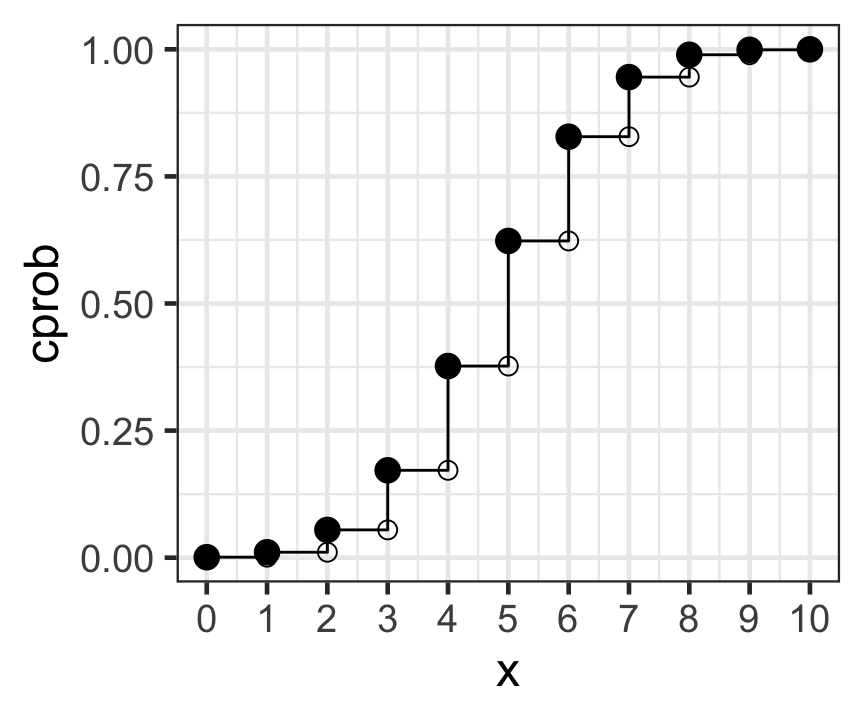

Exercise 3.4.1

  • Plot the probability mass function and cumulative distribution function of binomial distributions:

    1. \(X\sim B(10, .2)\), (ii) \(X\sim B(10, .90)\)

  • Plot the probability mass function and cumulative distribution function of Poisson distributions:

    1. \(X\sim Po(.2)\), (ii) \(X\sim Po(5)\)

  • Show three quartiles (first, second, and third quartile) in the appropriate graphs obtained for earlier questions

2 Normal distribution

  • Assume \(X\) follows a normal distribution, i.e., \(X\sim N(\mu, \sigma^2)\)

  • Probability density function \[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{1}{2}\big(\frac{x-\mu}{\sigma}\big)^2}\]

    • \(-\infty <x<\infty\), \(-\infty <\mu<\infty\), and \(\sigma^2>0\)

  • Standard normal distribution \[Z = \frac{X-\mu}{\sigma}\sim N(0, 1)\]

  • Cumulative distribution function of standard normal distribution \[\begin{aligned}P(Z\leq z) &= \int_{-\infty}^z \frac{1}{\sqrt{2\pi}}\,e^{-(x^2/2)}dx\\ & = \Phi(z)\end{aligned}\]

dat_norm <- tibble(
  x = seq(-4, 4, length = 1001),
  f = dnorm(x = x, mean = 0, sd = 1),
  F = pnorm(q = x, mean = 0, sd = 1)
)
dat_norm
#> # A tibble: 1,001 × 3
#>        x        f         F
#>    <dbl>    <dbl>     <dbl>
#>  1 -4    0.000134 0.0000317
#>  2 -3.99 0.000138 0.0000328
#>  3 -3.98 0.000143 0.0000339
#>  4 -3.98 0.000147 0.0000350
#>  5 -3.97 0.000152 0.0000362
#>  6 -3.96 0.000157 0.0000375
#>  7 -3.95 0.000162 0.0000388
#>  8 -3.94 0.000167 0.0000401
#>  9 -3.94 0.000173 0.0000414
#> 10 -3.93 0.000178 0.0000428
#> # ℹ 991 more rows

Normal distribution: PDF

ggplot(dat_norm) +
  geom_line(aes(x, f), size = 2) +
  theme_bw(base_size = 18)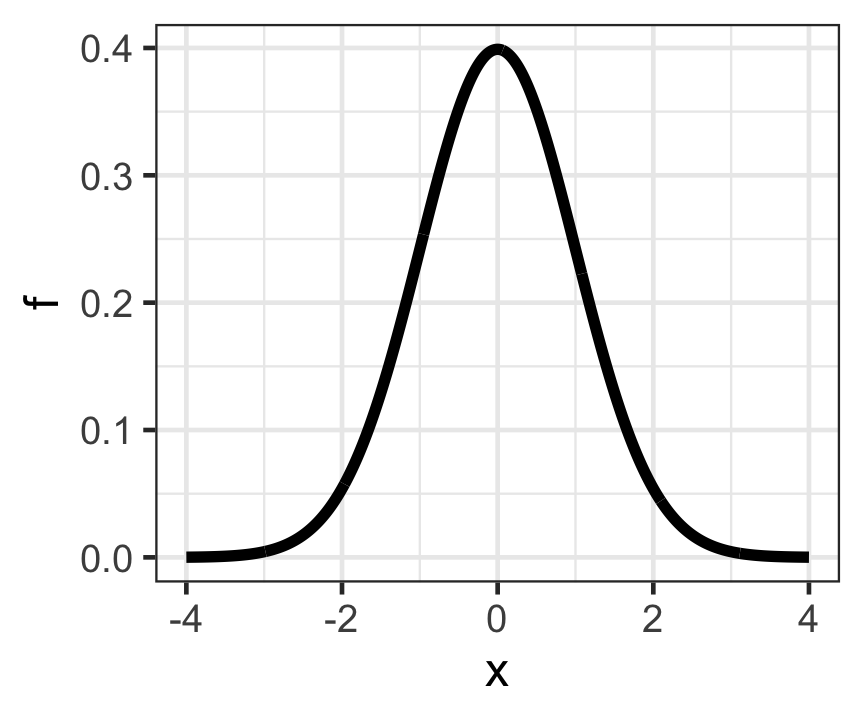

Normal distribution: CDF

ggplot(dat_norm) +
  geom_line(aes(x, F), size = 2) +
  theme_bw(base_size = 18)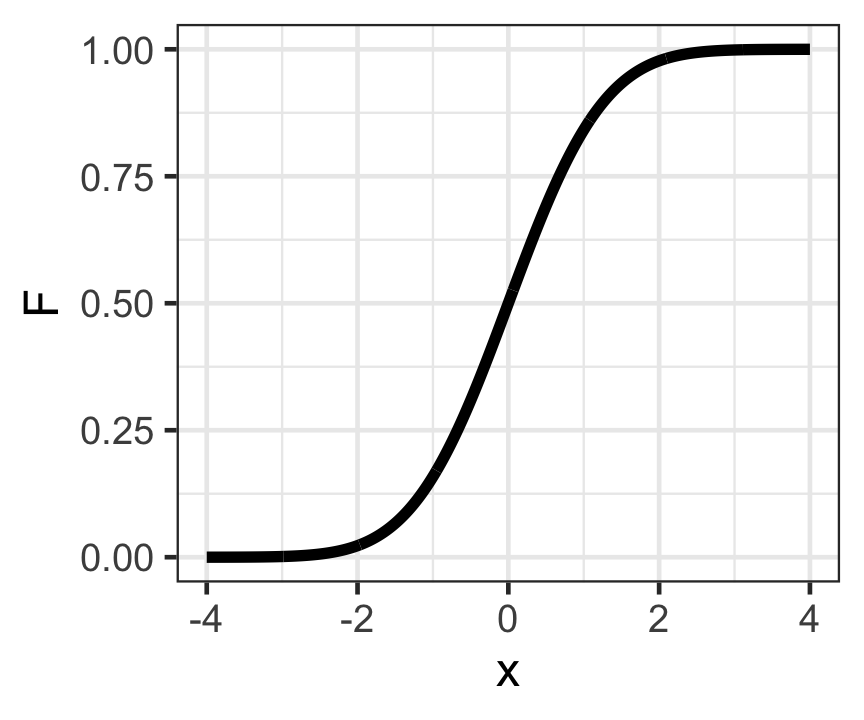

Standard normal distribution: PDF

ggplot(data = tibble(x = c(-4, 4))) + 
  stat_function(
    mapping = aes(x = x), fun = dnorm, 
    args = list(mean = 0, sd = 1), geom = "line") + 
  theme_bw(base_size = 18)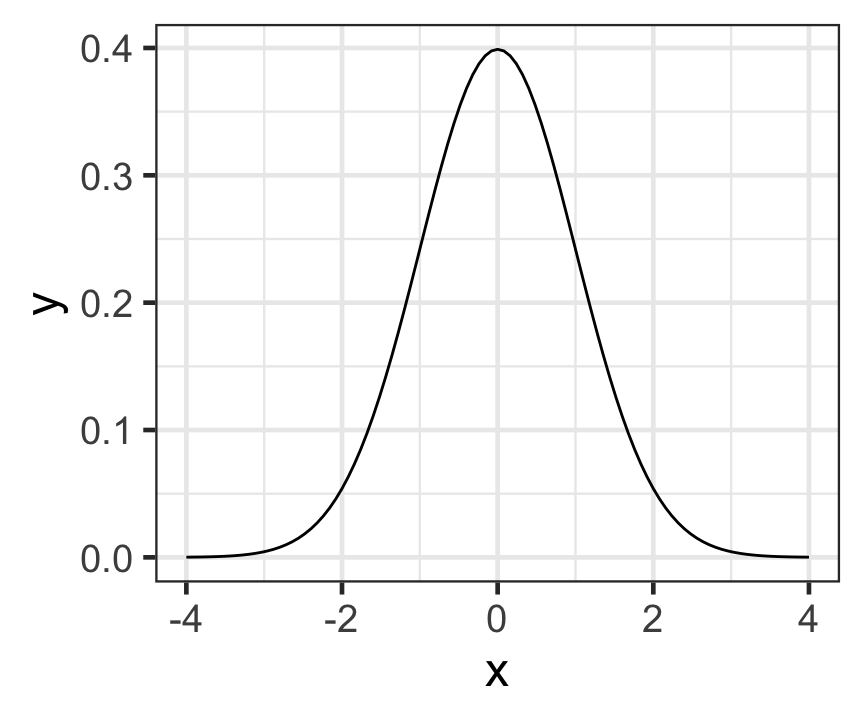

ggplot(data = tibble(x = c(-4, 4))) +
  stat_function(
    mapping = aes(x = x), fun = dnorm, 
    geom = "line") + 
  stat_function(
    mapping = aes(x = x), fun = dnorm, 
    geom = "area", xlim = c(1, 4), fill = "purple") + 
  theme_bw(base_size = 18)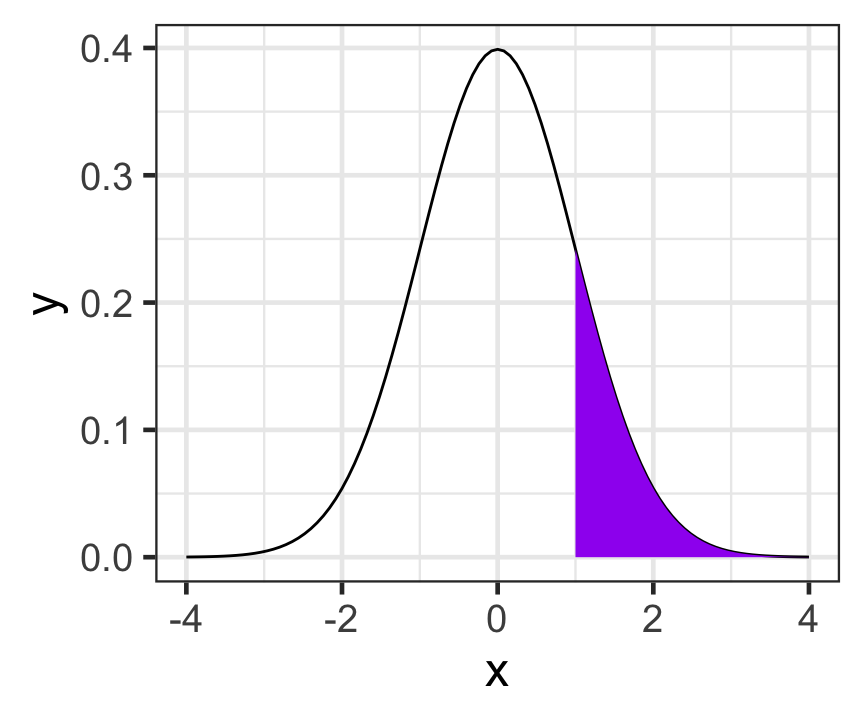

  • Unspecified args argument in stat_function() corresponds to standard normal distribution
ggplot(data = tibble(x = c(-4, 4))) +
  stat_function(
    mapping = aes(x = x), fun = dnorm, 
    geom = "line") + 
  stat_function(
    mapping = aes(x = x), fun = dnorm, 
    geom = "area", xlim = c(1, 4), fill = "purple") +
  geom_segment(
    aes(x = 0, xend = 0, y = 0, yend = dnorm(0)),
    col = "blue", size = 1.5) +  
  theme_bw(base_size = 18)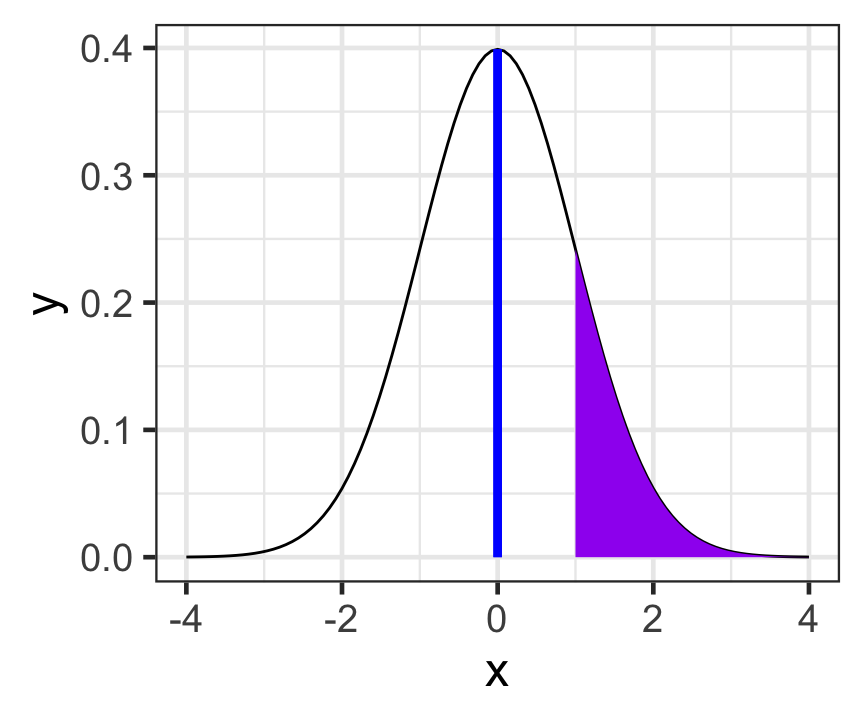

Exercise 3.4.2

  • Plot density and cumulative distribution functions of \(N(10, 7)\) and \(N(80, 40)\) distributions

  • Plot density functions of \(N(80, 40)\) and \(N(120, 40)\) distributions on the same plot

  • Plot density functions of \(N(80, 40)\) and \(N(80, 20)\) distributions on the same plot

Exercise 3..4.3

  • Plot cumulative distribution functions of \(N(80, 40)\) and \(N(120, 40)\) distributions on the same plot

  • Plot cumulative distribution functions of \(N(80, 40)\) and \(N(80, 5)\) distributions on the same plot

  • Plot density and cumulative distribution function of any other distribution that you studies in a course

Summary

  • Data manipulation and visualizations are briefly discussed at the level so that one can start working with tidyverse

  • The best way to learn R is by reading codes of the experts from their packages and books (Google is also helpful)

    • Knowing the experts for a specific topic is important!

  • From the beginning, try to use the “best practices” of coding as you write the codes for others (the future yourself is another person!)

  • Share your knowledge with others as R is free and a product of the volunteer contributions of others!